3D Topological Framework for Robust Digital Spatial Models

Concepts from the discipline of topology have proved to be useful tools in the management and analysis of digital spatial data, for the definition of spatial relationships, and for the maintenance of consistency.Although currently more visible in the GIS world, topology is equally important in CAD/AEC applications.To date, however, commercially available database software in the GIS field restricts topological storage to 2D only (or 2D with elevation values). Generally speaking, the CAD/AEC operates within a more restricted form of topology, with relationships such as overlap between objects being determined "on the fly." One of the critical issues in "closing the gap" between the disciplines of GIS and CAD/AEC is the requirement that representations of spatial objects be shared, and handled consistently by different software environments.

While some progress is being made in the definition and nomenclature of spatial primitives, a major inhibitor of consistency is to be found in the representations currently used to implement these primitives.The larger body of research in the field of vector representation of spatial data has concentrated on developing the mathematical model.This model typically is based on topological concepts such as the metric space, leading to rigorous definitions of concepts such as the boundary of a region, and connectivity between regions.

On the other hand, the digital implementation of the mathematical model is less well understood.The mathematical model pre-supposes the field of real numbers - which is dense and uncountably infinite, and therefore capable of representing a continuous region in a metric space.The computer, by contrast, represents the data typically as integers or floating point numbers, which are not dense, and are finite in their range of possible values.The effects of this approximation are far from trivial and not well understood.

For example: The union and intersection operations may not be associative, i.e. . More particularly, the result of depends on the order of execution.Thus a small effect, due to rounding errors, can lead to gross differences in result.

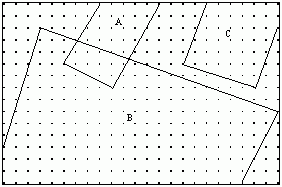
In this example, the union of A, B and C can result in a different configuration depending on the order of the operations.Forming the union between B and C first leads to a simply connected final result as below:

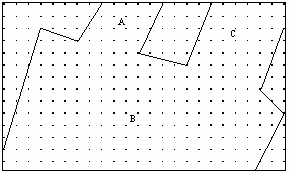
On the other hand, if is formed first, the rounding error in calculating point p causes the distance between B and C to exceed the tolerance.The result is a disconnected region:

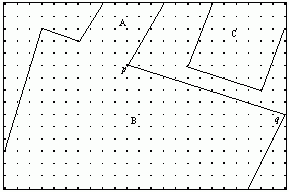
The language of GIS is couched in terms such as "union", "intersection" and so on, leading to an expectation that they should follow the normal mathematical definitions of these operations. Unfortunately, this is not always the case, and many implementations do not provide a closed, rigorous logic.

The Definition of Equality
The apparently simple question of whether two feature representations are equal, is often not well handled, and in many cases, the concept itself is not well defined.

Some concepts of equality could be loosely stated as:

a.The representations are "as good" as each one another in representing a real-world phenomenon. This could be interpreted as the requirement that the representations agree with each other to within some tolerance.This interpretation has the disadvantage of not being transitive.
b.The representations are identical in internal representations.For example, two polygons are defined by the identical point locations, in the same order.This is of value within a Database Management System, but not really of much use to the end user of the data.
c.Point set equality - the regions defined contain the same (transfinite) set of point locations. This is difficult to implement within current representations.

The International Standard ISO 19107 addresses this issue, but leaves the details to the implementer.

Representational Validity
Current spatial data storage implementations vary quite significantly in terms of the validation rules used for representations [Polygons: the unstable foundation of spatial modelling].This, taken in conjunction with the fact that data transfer is usually done in a way that precision is reduced, leads to problems in the sharing and re-use of data.

Current Approaches
In order to address the above issues, many approaches have been investigated.The following are earlier attempts described in literature.

Topological Encoding, and Milenkovic Normalization [Verifiable Implementations of Geometric Algorithms Using Finite Precision Arithmetic] are widely used in 2D and are capable of being extended to 3D.This approach could be described as "compiling" the topological relationships into the database structure, with rounding operations being done at the time of data entry.While this leads to consistency within individual layers of the database, operations between independent layers, or between data form different sources is problematic.
The Realms Approach [Realms: A Foundation for Spatial Data Types in Database Systems] addresses these issued by limiting the range of rounding effects, allowing support of a closed algebra (known as "ROSE").This requires the pre-calculation of intersections between all features on entry to the database, avoiding any logic failures at query time.The major disadvantage is that the complexity of feature representations increases with time.Adjustment operations such as datum changes would be problematic.
Constraint Databases [Constraint programming and database query languages] provide a rigorous approach, but processing technology has probably not yet reached the level required for a practical implementation in full generality.
The Rational Polygon [Complete Logics for QSR [Qualitative Spatial Reasoning]: A Guide to Plane Mereotopology]ⁱ provides the necessary rigor, but at the expense of a representation which grows in complexity with time.

Alternate Approach
An alternate approach, based on the rational polygon, and known as the "Regular Polytope," is suggested. It can be shown to support a rigorous and closed logic in 2D, 3D or higher dimensionality.This should enable the richness and power of the 3D representations currently available in the AEC/CAD environment to be combined with the large-scale consistency of GIS.

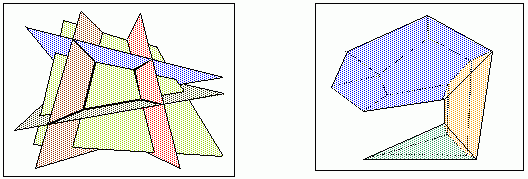
A Convex Regular Polytope can be constructed as the intersection of a number of half spaces, each defined by a plane in three dimensions.The convex polytopes can then be combined to form a general polytope.

It can be shown that this polytope representation provides a basis for a topological space.Further, it can be shown that the polytope is regular in the topological sense, of being equal to the closure of its interior.Note that the representation itself obeys the axioms of a topological space, rather than being an approximation to an idealised mathematical model.

The practicality of an approach such as this is to be judged against criteria such as:

Completeness of the logic in satisfying the requirements of spatial reasoning;
Support for concepts such as connectivity;
Practicality of implementation;
Data storage requirements;
Compatibility with existing approaches - for example topological encoding;
Completeness of representation; and
Ability to be standardised.

The regular polytope approach shows significant potential as a practical spatial data storage and retrieval strategy, viewed against these criteria.

ⁱLemon, O.and I.Pratt (1998b)."Complete Logics for QSR [Qualitative Spatial Reasoning]: A Guide to Plane Mereotopology." Journal of Visual Languages and Computing 9: 5-21.

Other installments published to date in this series:

In addition to the articles themselves, numerous readers have also posted comments on them (found at the bottom of each article).