|
Bill Thoen writes that steganography is any "technique of hiding
secret messages within other media, so that to all eyes but those of the sender
and intended receiver, no secret message appears to be present."
|
Introduction
|
There are plenty of ways to hide messages within images. This is
relatively easy because an image, being an array of pixels, typically contains
an enormous amount of redundant information. If you have ever compressed a
Windows bitmap (.bmp) file, for instance, you will have noticed that 90 to 99%
of the file disappeared. You can hide information in that extra space.
|
|
|
A bitmap and other common image files are in raster formats:
arrays of colored dots. This article focuses on the more challenging problem of reliably hiding
messages within vector data. Vector formats are used extensively by
Geographic Information Systems. They use sequences of coordinates
to represent points, lines, and regional boundaries on a map.
|
|
|
Why worry about the vector format when hiding messages in a raster format is
so easy? One application is protecting intellectual property.
When you have worked hard to produce GIS data, once it is released in an
electronic format, it's easy for somebody to copy it and re-use it without your
permission (or compensating you, either). By "watermarking"
vector data with a hidden copyright message or signature you stand a chance of
detecting and demonstrating commercial re-use of your data.
|
Purpose
|
|
Certain vector steganography techniques, as an incidental byproduct, will
also support change detection, data compression, integrity
checking, and integrated metadata. Change detection lets you know when a feature has been
modified. Data compression reduces the space needed to store
information. Integrity checking verifies that the data are correctly
stored and transmitted. Metadata is information about the data, such as
how it was developed, processed, projected, and so on. I find the idea of
hiding key parts of the metadata, such as accuracy and projection information,
in the figures themselves to be pretty cool.
|
Applications
|
|
Thoen describes several vector steganography techniques. This article
explores two of them, which I will call "jittering" and
"embedding." (This is a new subject, so I am not aware of any
standard terminology and have to make it up as I go.)
|
|
|
Jittering consists of making tiny changes in the vector
coordinates. These can be detected if all coordinates are rounded off in
advance. For instance, if you encounter a sequence of numbers like 3.142,
2.783, -1.000, and then suddenly see 5.9265358979324, it is
obvious something is going on. The information is contained in the extra
digits. Because those digits have low numerical significance--in the
example they would not change any single value by more than 0.001--their
introduction does not alter the number in any material way. Usually.
(We will get to the exceptions and problems later.)
|
Jittering
(Follow the link for detailed technical information and
source code listings.)
|
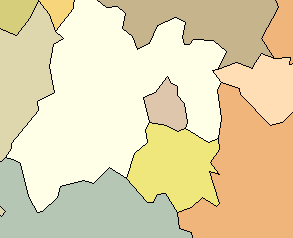
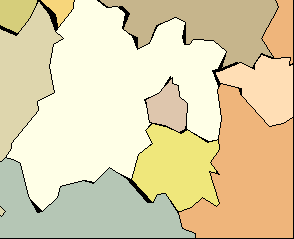
Close-up of the central Mexican states
|
Strongly jittered versions, showing how the vertices
move
|
Normally, jittering does not move vertices this
much. The motion has been greatly exaggerated to make this
illustration.
A full-featured implementation would
respect the topological relationships among these polygons, so that the
gaps and overlaps would not occur. The vertices would still move,
however, just as shown here.
|
 |
|
|
Embedding is a technique I developed to overcome some of the obvious
problems with jittering. Embedding consists of using the distances between
points to convey information. Usually it is accomplished by adding extra points to the
description of a vector figure. Since the points lie on the figure itself,
they do not change how it looks: they only change its internal
representation. The inter-point distances can transmit messages in many
ways. I discuss the choice of a good method below.
|
Embedding
|
|
In GIS applications, the greatest challenge for vector steganography is
coping with the effects of routine operations. To relate vector data to
real-world features, a GIS must "georeference" its figures.
Georeferencing operations include moving the figures around, rotating them,
changing their scale, projecting them (from the earth's surface to a flat map),
and "unprojecting" back again. A GIS may also modify figures to make them
topologically consistent and "clean." For instance,
the orientation of vertices might be reversed. Often this is done
automatically. All these operations usually introduce huge
changes in coordinates, thereby destroying any information contained in their
least significant digits.
|
The Problem
|
|
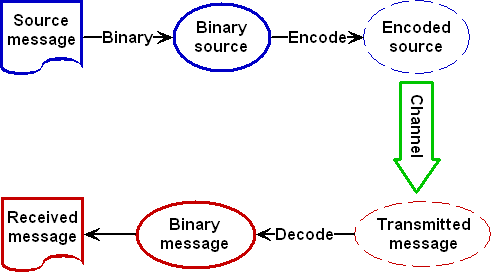
To cope with this, we need ideas from communications theory. From this
point of view, steganography is just another "channel" used to
communicate a source message to its destination. Any source message can be
viewed as a sequence of letters from an alphabet. On modern digital
computers each sequence ultimately is a binary string of zeros and ones: the
simplest possible alphabet, with two letters only.
As these letters are sent over the channel, they can be unpredictably
changed. Therefore something is needed to encode the source message
before it is sent and to decode it once it reaches its destination, in a
way that is relatively immune to changes made while in the channel.
(More about error-correcting codes appears at the Error Correcting Codes
page.)
|
Communications
theory
Claude Shannon developed this branch of
mathematics in 1948. Its practical applications were quickly
recognized.
For more information, see Robert McEliece, The Theory
of Information and Coding, 1977. Addison-Wesley, Reading,
Mass.
|
|
|
|
We can expect to pay a price for the ability to detect and correct channel
errors: the encoded source has to be redundant, so it will expand in size.
This is usually not a problem with raster steganography, because a raster image is such
a fat channel. The space for stuffing information into a vector channel is
so limited, however, that we must anticipate the need to compress the
source. Fortunately, many good source compression techniques are known and
readily available.
|
My ArcView software provides Huffman
compression simply to show it can be done within the GIS. Commercial
products, using more sophisticated techniques, will do a better job
of compressing messages.
|
|
Chances are, a vector channel will be public: in many of the
applications, anybody could have access to our GIS data. We will want to
make our message secure, so that it cannot be understood even if it is
detected in the channel, and we might want to authenticate it, so that
the intended receiver can verify it came from us. Again, many good
techniques for security (encryption) and authentication (digital signatures) are
known and readily available.
|
Rivest, Shamir, and Adleman published their seminal
paper on this subject in the Communications of the ACM in 1977. See http://www.rsasecurity
.com/rsalabs/faq/
for more information.
|
|
From now on, therefore, we may just as well assume the source message has
been digitally signed and encrypted and that the received message might have to
be decrypted.
|
The remaining challenges are unique to the vector channel. First, since
this is supposed to be hidden communication, it would be nice to disguise the changes
made, however small they might be. Making them look random would
work. At first blush, this is not a problem, because any well-encrypted
source is already going to look very random, and it will stay random even when
converted to binary. However, the randomness will be lost by the
error-correction encoder. The process of making a message redundant
introduces a lot of structure--evident patterns--into the signal. This
might be easily detectable by software that probes vector data for possible
hidden messages. Therefore a special randomization step is needed just
before the signal enters the channel (that is, just before it is written into
the vector figures). For details please see Randomizing a Message.
|
The Challenges
I accomplish the "special randomization" by
masking the message bits with a deterministic sequence of pseudo-random
numbers using a decent generator. The same procedure conveniently
serves to reverse the process when reading the message.
|
|
Second, and this is the most difficult part, is that the kinds of changes
that can happen to a message embedded in a vector figure are different than
those that communication theory knows how to cope with. Most
communications channels are pipes of some sort-- telephone wires, network
connections, radio signals, and so on--that convey the message bits. Along
their way, these peripatetic bits encounter monsters of the ether, such as
noise, cosmic rays, and so on, which prey on electric signals, sometimes
changing them or even obliterating them beyond recognition. Usually, these
changes occur pretty randomly, or at worst in random bursts.
|
|
On the other hand, a vector figure might be moved, reprojected, get sliced up, merged with
another figure, reversed in orientation, or even have a few vertices added or removed. You might
argue that by then the figure is hardly worth protecting. Well,
maybe. If you try to read a message out of a figure and find it
obliterated, at least you have detected a change. But in other
applications, such as protecting intellectual property, you probably don't want
relatively minor or routine alterations to be considered "new
works." If you have accurately surveyed a pipeline or road map, for instance, you
should be able to protect your rights to its shape, and guarantee its accuracy,
regardless of what projection it is mapped in. Moreover, it would be nice
to protect even individual portions of the line.
|
Map-makers purposely introduce tiny errors, such as
"trap streets," into hardcopy maps to obtain copyright
protection. Vector steganography can serve to make invisible
"trap streets" with the same effect..
|
|
In such applications, jittering just won't cut it. This is what
embedding was invented for.
|
More about embedding
|
|
The key to embedding is to consider what remains after you move, project, and
otherwise slice and dice a figure. Although the coordinates change, and
distances, angles, and areas change, the shape approximately remains the same.
|
|
Here's a fanciful way to embed a message within a vector
figure, the "handwriting" technique:
|
|
|

|
|
(I have not tried too hard to hide the message, so you can see what's going on, but in
principle it could be shrunk to invisibility without trouble.)
|
|
|
Even after unprojecting and reprojecting with a very bad projection, we can
recognize the message:
|
|
 |
I am not seriously proposing that anybody should
actually use this method! The disadvantages listed below essentially
rule this out as a practical technique.
|
| These figures show each segment
of the outline in a different (random) color so you can see where the
vertices are. |
|
|
The original figure consisted of 112 segments. Embedding the
10-letter message created a figure with 853 segments. The figure's
boundary now has some self-intersections, which isn't very good, either. |
|
|
This handwriting technique, although somewhat silly, has most of
the characteristics we would like vector steganography to have:
|
|
 | It is straightforward to encode messages into the channel and decode
them again. |
 | Messages will survive heavy abuse in the channel, including moving,
rotating, rescaling, skewing, reprojecting, and even some random
vertex movement, insertion of vertices, and chopping of the figure
into not-too-small pieces. |
 | Messages can be hidden by making them extremely small compared to
the rest of the figure. |
|
|
| The
disadvantages of handwriting, though, are important: |
Jittering has potential
self-intersection problems, too: if two vertices are very close, then
jittering can twist up the figure. This problem can be handled by
jittering only the least significant digits in the coordinates.
|
 | It is inefficient: a large number of new vertices must be introduced
to transmit each character. (If this page took a while to load,
the previous figure is the reason why!) |
 | It is easy to detect and obliterate: any program that
"cleans" figures by eliminating slivers or
self-intersections will accomplish that. |
 | It ruins the shape by introducing self-intersections; this can be a
problem for subsequent geographic analysis carried out in software. |
|
| What I
mean by "embedding" is any variant of handwriting that overcomes
these problems while maintaining the good characteristics. |
|
| The
approach that appears the most promising either doesn't change a figure's
shape at all, or it changes it in a natural, undetectable way. In
its most sophisticated form ("splined embedding") it is
completely undetectable and, as a side-effect, can even improve the
representation of many geographic features. |
|
| The
simplest form of embedding, as I propose it, is to insert sequences of points
along the line segments that form a vector figure. The first point
establishes a reference length. The distances to subsequent points
will either equal the reference length or exceed its length by some factor
(which I call the "strength" of the embedding). For
example, if the reference length is four inches and the embedding strength
is 1.0, then the factor used is 1 + strength = 2.0 and the lengths will be
four inches or eight inches (2.0 times four inches). |
These are world inches, not inches on
the map!
|
| The
lengths will correspond to bits in the signal: a long length for a 1, a
short length for a 0. Every message will be preceded by the
reference length (encoding a zero) just to get things started. |
|
| Decoding
an embedded message allows for some "slop" in the relative
lengths. This is what protects the message from changes brought
about by GIS operations. Let's suppose that somehow you can find the
beginning of the message. The first length is interpreted as the
starting 0. Subsequently, any large increase in the next segment
length encountered is interpreted as a 1 and any large decrease in length
is interpreted as a 0. By focusing on increases and decreases, the
decoder does not depend on the exact preservation of relative lengths. |
I am skipping over an important detail
here. It's not so easy to find the beginning of the message!
The solution is to bracket the message by a specific sequence of bits that
is highly unlikely to appear by accident. These
"sentinels" show where the message begins and ends.
Between 24 and 48 bits should suffice for each sentinel.
|
| As a tiny
example, let's send a message consisting of an ASCII "A".
Its binary value is 0100 0001. The embedded message must begin with
a zero, so we need to encode the sequence 0 0100 0001. Let's use the
longest side of the figure for the embedding, so that we can keep the
reference distance reasonably large. (Super-tiny segments in a
figure might give away the presence of a message.) Suppose this
figure is part of a road map and the longest segment is 110 meters.
Using a strength of 1.0, we would choose a reference length of 10 meters
and encode the zeros as 10-meter segments and the ones as 20-meter
segments. Here's what the embedded message looks like: |
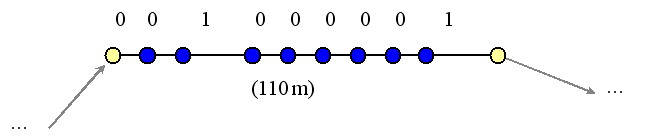 |
| The yellow
(end) vertices were originally in the figure. The blue ones have
been added to transmit the binary signal. They will not be visible
when the figure is drawn. |
|
| If this
figure gets distorted, the message can still be read provided the relative
lengths along the message do not change by too much. The higher the
strength of the embedding, the more resistant the message becomes to such
distortions. |
|
| There are
plenty of problems with the simple method just shown, but most of them can be
overcome. |
|
Problem: It's pretty wasteful to devote one vertex to
each bit of the signal: the two coordinates of a vertex require between
64 and 128 bits, depending on the GIS. Solution: We
aren't limited to just two lengths. For instance, we could use
lengths of one, two, four, eight, 16, 32, 64, and 128 times the
reference length to squeeze three bits of information into each new
vertex. We can get far more than that by using weaker
strengths. For example, a strength of 0.05 would be good enough to
resist the effects of most reprojections; using lengths up to 25 times
the reference would let us put eight bits of information into each new
vertex.
|
The ArcView software I wrote does not
use multiple lengths, and so is quite inefficient. It does allow you
to specify the strength.
|
Problem: Embedding looks like it would be easy to
detect, because it creates sequences of vertices with perfect 180 degree
angles. Solution: Instead of putting the new vertices
along a straight line between two original vertices, put them along a
nice smooth curve, such as a spline. This solution would look very
much like the result of a common, innocuous GIS operation,
"densification," used to improve the appearance of figures.
|
The ArcView software does not provide a
splined solution.
|
Problem: Embedding might require extremely tiny
reference lengths. For instance, a detailed outline of the state
of Texas requires over 1000 points, of which the longest segment is only
a few kilometers. A moderate-size message might require 1000 or
more bits, forcing the reference length down to a few meters or
less. Solution: You don't have to limit the embedding
to a single side of the original figure. You can turn corners,
either by incorporating the original vertices into the embedded signal
or by using special lengths to signal when the original vertices should
be skipped, if they lie in the wrong position.
|
The ArcView software does not attempt to
go around corners. It limits the embedded message to the longest
side of the original figure.
|
Problem: Any automated procedure for
"thinning" or "weeding" unnecessary vertices will
obliterate any embedded message. Solution: Splined
embedding will prevent the weeding of redundant vertices (those with
180-degree angles). However, an aggressive weeding routine will
eliminate various vertices even along splines. There is not much
we can do to defend against that, except to note that weeding reduces
accuracy and cartographic quality, and so constitutes a fundamental
change in the figure. One can do only so much to protect a hidden
message!
|
|
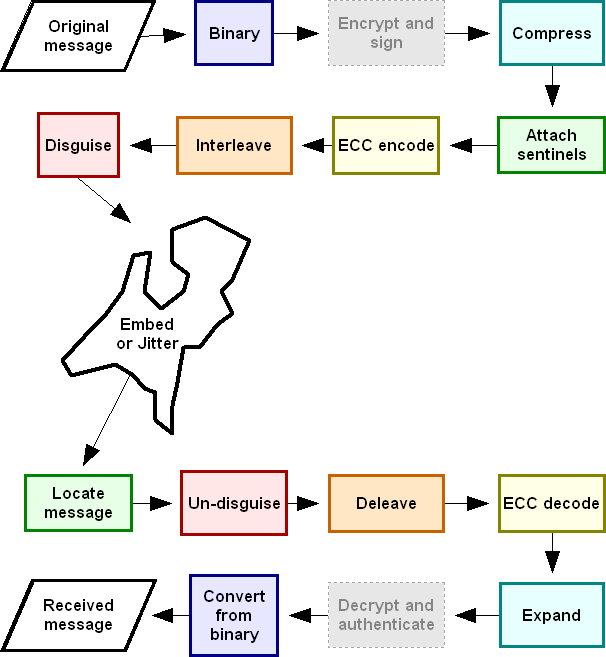
| A
robust, practical implementation of vector steganography will have many
steps. Here is a guide: |
The "encrypt and sign" and
"decrypt and authenticate" operations are grayed out to indicate
I have not implemented them in the ArcView prototype.
Notice the asymmetry between the writing
(top half) and reading (bottom half): to maintain a perfect disguise and
to make error-correction effective, the sentinels have to be added before
these operations are performed. On the other hand, the sentinels are
used to locate the message within the vector figure, which has to happen
before any other part of the reading step. How are the sentinels
found? By inspecting the figure point by point, undisguising and
decoding a small number of bits at a time to see whether they match the
sentinel.
This asymmetry is something that writing
the prototype taught me. Unfortunately, I figured it out too late to
change the design: the prototype adds the sentinels just before embedding
or jittering. This is not as good a solution..
|
 |
| There
remain some potential difficulties with any kind of vector steganography,
whether it is implemented by jittering, embedding, handwriting, or some
other means. Let's consider a few of these. |
The remaining difficulties
|
| First,
steganography is not built in to any GIS. So how does one acquire
this capability? The obvious solution is to use the built-in
scripting capabilities found in any reasonable GIS. However, scripts
usually run slowly--sometimes hundreds of times slower than compiled
programs--and steganography is a complex process requiring a lot of
computation. This is a legitimate concern, which is why Thoen
scripted a jittering solution in MapBasic (for the MapInfo GIS) and I have
scripted (in Avenue for the ArcView 3.x GIS) a comprehensive solution
including source compression, error-correcting coding, and message
encryption, implementing both jittering and a simple form of
embedding. Both systems are prototypes and neither is perfect, but
they serve as proof of concept and address some of these practical
issues. In particular, the Avenue solution is robust enough to go to
work now and its execution speed is reasonable: typically it takes less
than a second to write or read a 254-character message in a moderately
complex feature of several hundred vertices. |
The execution time depends on what
features you are using. The speed quoted here is for compressing,
adding error correction, burst error correction, and randomizing the
message.
|
| Second,
GIS datasets often get reformatted. Conversion from one format to
another can completely destroy a jittered message, as Thoen and I
discovered in one early test. Fortunately, an embedded message
survives reformatting easily. |
Not all conversions are this bad, but
some can be.
|
| Third,
most GIS datasets contain information about how neighboring regions abut
each other or how portions of networks attach to each other.
Changing coordinates willy-nilly, as in jittering, can destroy these
topological relationships. Although our prototypes have not
accounted for this, they readily could be using well-known techniques, such
as representing polygons as sequences of arcs shared with neighboring
polygons. This would eliminate the gaps and overlaps evident in the
jittering illustration above and would make the splined embedding solution
truly workable. |
|
| There
now exists software for MapInfo and ArcView 3.x that will let you hide
messages in vector data and read them back again. This has many
potential applications, including copyrighting, watermarking, data
compression, change detection, authentication, and integrity
checking. The algorithms can be adapted for any vector GIS and
improved to create a truly robust, flexible, efficient system that
provides all these benefits.Click on this link HERE for a dowloadable (100K) ArcView 3.2a project file.The project contains two dialogs and a lot of scripts, nothing else.It is guaranteed virus free.(It is not, unfortunately, guaranteed bug free!) The sidebars to the article above provide a lot of guidance for understanding these scripts.Eighteen of the scripts are test drivers that exercise most of the core routines implemented in the other scripts.Running and studying these would be a good place for the interested reader to begin.The scripts have all been protected (and indemnified) with a GNU copyleft,
as available at www.gnu.org/copyleft/gp1.html .(It would be
the first readable text you encounter if you open the project file in a word processor.) |
Conclusions
|






