Imagine you had collected 1,000 census data points in 1998 from a fixed area.In 1999 you collected 2,000 points over the same region, in different locations.How will you compare the 1999 and 1998 points to see increasing or decreasing trends? It is not possible to use simple database math to subtract one year from the other because the tables do not line up.The solution is to convert both point files into continuous grid layers that can easily be overlaid and compared.Point files are converted into grids by interpolation.It is my hope to take some of the mystery out of this operation, pique your interest in grid mapping and show off some features of surface generation software in the process.
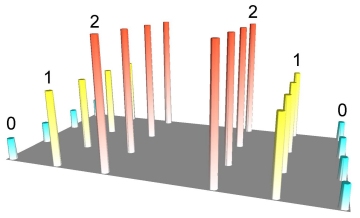
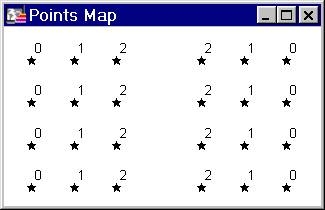
Let us start with a simple point file.24 points are arranged in a regular fashion with attribute values ranging from 0 to 2 as shown below.
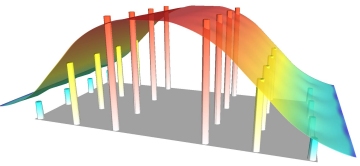
The attribute can be as varied as a dollar value or the signal strength level of a cellular phone.As long as it is numeric it can be represented in 3D form, as depicted below.In fact, the image is actually a rendered grid.The grid was generated using IDW interpolation, sampling only one data point (to exactly honor the data values), using a very small display radius equal to the width of a single column.Rendering this sort of sparse grid creates a unique thematic map akin to a 3D bar chart.
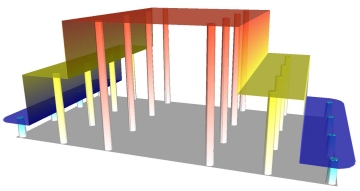
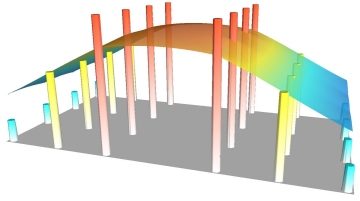
Of course the main reason for using grids is to build a continuous surface that connects the data points in space, effectively removing gaps in the representation of data and facilitating comparison of datasets.
To fully take advantage of this technology one must have a clear mental picture of what grid surfaces are, what type of surface best represents the intervening area between known data points, and which interpolation technique must be used to generate an appropriate surface.While I cannot answer all those questions in this article, I can give you a taste of what's possible and start you thinking in 3D.
There are two properties that must be determined before choosing an appropriate interpolator for a dataset:
- How reproducible is the data (a function of the collection and analysis techniques)?
- Does the data point represent only a value at that point in space, such as an elevation point, or does it represent a property from a wider area such as an enumeration area centroid?
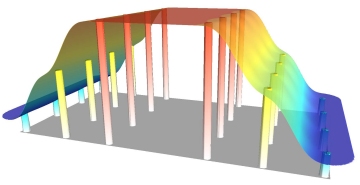
If the rate of change between regions surrounding a point is too abrupt, then it is possible to adjust the Natural Neighbor interpolator to make a gradual sloped surface between the points.This includes minor smoothing and limiting the maximum and minimum values of the surface so that no part of the grid has a value beyond the range of the original point data.
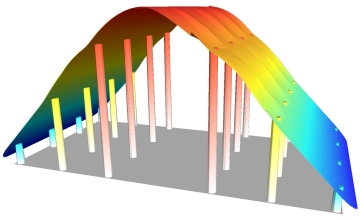
If the data points represent elevation values of a buried bedrock surface that acts as an oil or gas trap, then we may require the interpolated grid surface to curve above or below the range of the sampled data points.It isn't possible to guarantee that exploratory drilling will intersect the apex of the dome and thus it is necessary to model this curvature as shown below.
Understanding the reproducibility of the data determines whether or not we need the interpolated surface to exactly pass through the data points or we require a surface which simply represents the general trend.Inverse distance weighting is one interpolation method that performs a moving average or "smoothing" of the data.For instance, many bulk soil chemistry analyses produce fairly reproducible results.The example below shows a slightly smoothed surface generated by Inverse Distance Weighting.The high and low data points are not exactly honored.
On the other hand, analyzing for gold requires sieving out a very small amount of material from the soil sample and dissolving it in acid and vaporizing it in the flame of an atomic absorption spectrometer.Not surprisingly, if you return to the area where the soil sample was taken, dig another hole and repeat the process, chances are that it will yield a rather different result (the "nugget" effect).In this case, it would be appropriate to represent the data points with a grid which heavily smoothes the data, showing the general trend but masking the irreproducible results.Interpolation by kriging is one such method, while it can also be used as an exact interpolator.The example below uses kriging with an option to smooth the data heavily.
So there it is.Build a simple data set and begin experimenting.Vertical Mapper has many grid generation and visualization tools that make it easy and intriguing to explore and understand the effect of small changes in interpolation settings.A whole new world of benefits awaits those who can visualize their data as a 3D surface!