1. INTRODUCTION
In
the early days of sailing, the main objective of a ship navigator used to be
simply to take a ship from one point to another using as safe a route as
possible. This used to be done on the grounds of personal experience and
knowledge of the navigator himself, knowledge of land objects and celestial
bodies, as well as the knowledge of periodicallity of hydrometeorological
conditions. Multiple sailing following the same route and experince thus gained
were the basis for safe ship guidance.
With
the development of knowledge, this task became more complex and the need for
ship guidance arose, not just safe guidance but also the one to take a specific
route in the least time possible. This led to the development of methods for
position coordinates defining using objects at sea, on land, in space and
celestial bodies. At the same time, sophisticated equipment was developed for
establishing ship-to-ship and ship-to-shore communicatin, as well as the
calculation techniques for the elements of sailing.
Thanks
to systems of position fixing and communication, all the necessary elements for
route optimisation are now avaliable to a navigator. With the aid of computer
programes, by entering departure and arrival position coordinates, assuming
favourable hydro-meteorological
conditions in the sailing area, the navigator can determine all the elements
relevant to sailing. In case the departure and arrival positions are far apart,
the navigator will choose great circle or orthodrome navigation, if they are close,
he will choose rhumb line or loxodrome navigation, and if at higher latitudes,
i.e. at areas possibly dangerous to navigation, he will choose combined
navigation.
The
paper presents the problem of route optimisation in practical navigation, by
determining the optimal number of waypoints to which an orthodrome is divided
and between which the loxodrome navigation is done. The optimal number of
orthodrome waypoints depends upon geographical coordinates and the distance
between the end points.
2. ORTHODROME AND LOXODROME
Sailing
between two positions far apart in vast sea areas is possibly done in three
ways: orthodrome, loxodrome and combined navigation.
The shortest route from departure position to arrival
position is a shorter section of the great circle arc, i.e. orthodrome. Such
navigation is difficult to achieve since the orthodrome cuts the meridians at
different angles. It would require constant, precisely defined, change of
course.
In the case ship course is constant, which is easily
achievable in practice, the ship follows a curve asymptotically approaching the
pole. Such a curve on the surface of the Earth is called a loxodrome.
In the case of combined navigation, a standard
orthodrome is replaced by two-orthodrome tangent to the boundary parallel and
one loxodrome between them. By applying the techniques of combined navigation,
the areas of dangerous sailing, which could be reached by following strictly
the orthodrome navigation, are avoided.
3. CHARACTERISTICS OF THE ORTHODROME
Orthodrome is the shortest track on the surface of the
earth. Therefore, the aim of orthodrome navigation is the least track and time
between two distant positions, resulting invariably in cost-effectiveness.
Since strict orthodrome navigation is difficult to achieve in practice, it is
divided into a definite number of waypoints between which the loxodrome
navigation is applied. The difference between the sum of such loxodrome
distances and orthodrome distance represents the saving in way length, which
would otherwise, in case of strictly applying orthodrome navigation, be
achieved. This saving may be expressed in percentage (1):
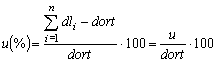(1)
Where
u(%) - represents the relative way length saving
expressed in percents,
dl
represents the loxodrome distance between adjacent waypoints,
dort
represents the orthodrome distance between end points and
u
represents the difference between sum of loxodrome distances and orthodrome
distance.
3.1. orthodrome distance
Orthodrome distance can be calculated by applying
three patterns of sphere trigonometry: cosine theorem, square sine of the
semi-angle and square sine and cosine of the semi-angle. In this article, the
first case is considered, since the determination of orthodrome distance using
cosine theorem of sphere trigonometry is the most appropriate one for computer
calculation. According to this theorem, cosine of one side of the triangle is
equal to the product of cosine of the other two sides increased for the product
of the same two sides and the sine of the angle between them (see Figure 1):
(2)
Since the complements of departure and arrival
position latitudes are:
and 
, the expression (2) may be transformed as:
(3)
i.e., into the explicit expression for orthodrome
distance (dort):
(4)
When using this formula, trigonometric function signs
are to be taken into consideration, i.e. their products, which is important
when sailing across the Greenwich and/or the Equator. In such cases, the first
product is endowed with a minus sign, which results from sphere triangle of
orthodrome with its vertex at the North Pole.
|
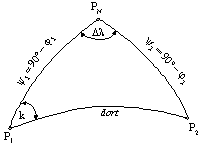
Figure 1. Orthodrome sphere triangle taken from the Earth |
|
|
Legend: P1, P2 departure and
arrival positions, PN North Pole, j1, j2 departure and arrival position latitudes, y1, y2 complements of departure and arrival position
latitudes, Dl difference between longitudes of arrival and
departure positions, k initial orthodrome course and dort orthodrome distance |
|
3.2. INITIAL
ORTHODROME COURSE
Initial orthodrome course does not have great
practical significance; nevertheless, it is necessary for further calculations.
It is used in quadrant semicircle division, i.e. may take the values between 0
and 180 degrees. The value of the initial orthodrome course may be defined by
the sine theorem of sphere trigonometry, according to which the relation of the
sine of the sides and the opposite angles in a sphere triangle is equal to:
(5)
Having the given proportion, it is possible to define
the initial orthodrome course by:
(6)
When using this formula, care should be taken when
defining the sign of the initial course, i.e. the sailing direction. However,
by using appropriate computer programs and generalizing the expression for
initial orthodrome course, the above-mentioned formula gives precise results.
3.3.
ORTHODROME WAYPOINTS DEFINING
Strictly following the orthodrome is not achievable in
practice, because of the necessity for constant course changes, for small,
precisely defined values. Therefore, a certain number of orthodrome waypoints are
to be selected and then used as points between which it is to be sailed with
constant course. Thus, the orthodrome is approximated by way of a number of
shorter loxodromes, the common positions being the determined waypoints.
Upon the determination of waypoints geographical
coordinates, they are drawn onto a Mercator chart; the loxodrome courses to be
followed are got by connecting them. In this paper, the courses, as well as the
appropriate loxodrome distances, were determined by calculation.
For the calculation of orthodrome waypoints we use the
right-angle sphere whose vertices are the pole closer to the orthodrome vertex,
orthodrome vertex and the observed waypoint (Figure 2). The waypoints may be
selected symmetrically to the orthodrome vertex, or else the orthodrome is
divided into a definite number of equal sections and thus waypoints coordinates
are defined. The division is arbitrary and may be 1, 2, 3... degrees, depending
on the orthodrome length. In this article, the other approach was used since it
is more appropriate to computer application.
|
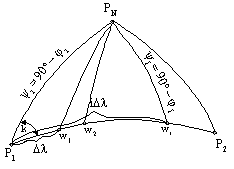
Figure 2. Sphere triangle of orthodrome waypoints on Earth |
|
|
Legend: P1, P2
departure and arrival positions, PN North Pole, j1, ji departure and "i" position latitudes, y1, yi complements of departure and "i"
position latitudes, Dl difference between longitudes of two neighbor positions, iDl difference between longitudes of i and departure position and w1, w2,
,wi waypoints of orthodrome |
|
Geographical latitude of orthodrome waypoints may be defined
by using the cone theorem for the side of a sphere oblique angle triangle as
follows:
(7)
Where
- Represents
the waypoint latitude,
- Represents the distance between the adjacent
waypoints,
- Represents the latitude of the starting waypoint,
k - represents
the initial orthodrome course and
i - represents
the ordinal number of the waypoint, n
being the total number of waypoints.
Using the sine theorem of sphere trigonometry and
sphere oblique angle triangle of waypoints, it is possible to define the
expression for geographical longitude of waypoints as follows:
(8)
Where 
equals to:
(9)
Once the orthodrome waypoints coordinates have been
determined, it is possible to define the associated loxodrome courses and the distance
for each pair of adjacent waypoints. After that, it is possible to determine
the sum of loxodrome distances and its difference from orthodrome distance,
i.e. determine the number of orthodrome waypoints for which this difference has
the least value, thus achieving way length saving.
3.4. Dependence of way length
saving on orthodrome division steps
After having studied a considerable number of pairs of
end points, arbitrarily selected on lower latitudes (30 60 degrees) and being
far apart (7, 8 and 9 thousands Nm), it became evident that the way length
saving in case of strictly following orthodrome navigation has the tendency of
decreasing when increasing the number of orthodrome steps. However, it is a
very rough estimate, since saving vary considerably, i.e. has significant ups
and downs for different steps of division.
With the aid of a program created in program language Matlab (Algorithm 1, Appendix 1), it is
possible to determine the optimal number of waypoints for which the saving is
minimal in case of strictly following orthodrome navigation, as well as the
associated courses and loxodrome distances.
Dependence of way length saving, in the case of
strictly following orthodrome, on the orthodrome division step was obtained by
statistic analyses (10):
(10)
Where
p
represents way length saving in the case of strictly following orthodrome,
x
represents the orthodrome division step and
a,b,c represent
coefficients.
3.5. COORDINATES OF ORTHODROME
INTERSECTION WITH THE
GREENWICH
In the
cases when orthodrome intersects the Greenwich, the simplest method of defining
waypoints is to divide the orthodrome into two sections, one from the starting
point to Greenwich and the other one from Greenwich to the end point. The same
rules usually used in defining waypoints coordinates are then applied to those
two segments. The latitude of the intersection with Greenwich may be defined on
the basis of sphere triangle diagrams 
,
and 
(Figure 3).
|
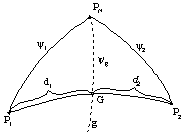
Figure 3. Scheme of sphere triangles as the basis for determination of orthodrome
and Greenwich intersection coordinates |
|
Legend: P1, P2 departure and
arrival positions, PN North Pole, g Greenwich, G point of orthodrome intersection with
Greenwich, y1, y2, yg complements of P1,, P2 and
G position latitudes, d1 distance between departure and
intersection position and d2 distance between intersection and
arrival position |
Applying the sine theorem of sphere geometry, for the
triangles 
and 
, the following equations result:
(11)
(12)
From proportions (10) and (11), as well as on the
basis of the orthodrome distance being equal to the sum of distances 
and 
, by applying the appropriate trigonometry transformations,
it is possible to obtain a definite expression for geographical latitude for
the intersection with the Greenwich:
(13)
where the longitude of the intersection point with the
Greenwich,
, is 0 to 180 degrees.
Program code for determination of jg is given in
Algorithm 2 (Appendix 1).
3.6.
COORDINATES OF ORTHODROME INTERSECTION WITH THE EQUATOR
When determining the longitude of intersection with
the Equator, the square triangle 
represented in the Figure 4 is used.
|
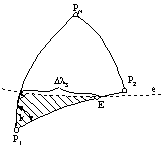
Figure 4. Scheme of sphere triangles as the basis for determination of orthodrome
and Equator intersection coordinates |
|
|
Legend: P1, P2 departure and
arrival positions, PN North Pole, e Equator, E point of orthodrome intersection with Equator
and Dls longitude of orthodrome intersection with
Equator |
|
Since the meridians are normal to the Equator, it is
possible to define the longitude of the intersection with the Equator on the
basis of right angle sphere triangle, i.e. by applying Nepper rules the
following is obtained:
(14)
(15)
While determining the longitude of intersection point,
the sailing direction must be taken into consideration.
Program code for determining coordinates of orthodrome
intersection with Equator is given in Algorithm 3 (Appendix 1).
4. COMBINED NAVIGATION
A drawback regarding orthodrome is that its vertex is
at higher latitudes than the latitudes of departure and arrival positions 
and 
. In case the orthodrome vertex is between departure and
arrival positions, by strictly following the orthodrome navigation some area
dangerous to navigation could be reached. In such cases, a boundary parallel is
chosen which a ship is not to cross during navigation. The selection of a
boundary parallel is done in accordance with hydro-meteorological conditions in
the sailing area.
Combined navigation consists of the following:
1. It is
navigated along the orthodrome with its vertex on the boundary parallel,
2. Then it is
navigated along the parallel until the position representing the vertex of
other orthodrome is reached and
3. Finally, it
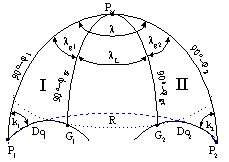
is navigated following the second orthodrome to the final position (Figure 5).
|
Figure 5. Geometric representation of
combined navigation |
Legend:
P1, P2 departure and arrival
positions,
PN North Pole,
j1, j2 departure and arrival position latitudes,
jg boundary parallel latitude,
l difference between longitudes of arrival and
departure position,
lg1, lg2 longitudes of intersection points,
k1,k2 orthodrome courses,
Do1,Do2 orthodrome distances,
G1,G2 points of intersection
between orthodrome and loxodrome, i.e. boundary parallel and
R loxodrome distance
If through the tangent positions of orthodrome and
boundary parallel 
and 
meridians are drawn, two sphere triangles are obtained (I,
II) with the meridians of 
and 
points being normal to orthodrome 
and 
, as well as to the loxodrome course along the parallel. From
orthodrome triangles II, by applying the Nepper rules, the necessary elements
of both orthodrome and I can be calculated. The essence of the problem is the
determination of geographical coordinates of positions 
and 
, orthodrome distance run 
and 
, loxodrome distance run R, as well as the angles 
and 
. From the diagrams of sphere triangles on Figure 5, the
following relations for determination of the difference between longitudes of
endpoints and intersection with the characteristic meridians are found:
(16)
(17)
Orthodrome distance runs 
and 
are defined according to the following expressions:
(18)
(19)
Departure and arrival position angles are as follows:
(20)
(21)
On the basis of these elements, the coordinates of
both orthodrome waypoints with their vertices in the positions 
and 
may be defined. Navigation along a parallel is characterized
by:
(22)
(23)
The course taken along the parallel is either 90 or
270 degrees, and the distance run equals to span R. Total distance run between
departure and arrival positions is as follows:
(24)
Where
D
represents the distance between endpoints,
represents the first orthodrome distance,
- the second orthodrome distance and
R - the
distance as the result of navigation along the boundary parallel.
Thus, in combined navigation an orthodrome is replaced
by two orthodrome tangent to the boundary parallel and one loxodrome. As a part
of this program (Algorithm 4, Appendix 1), the problem of combined navigation
has also been tackled, i.e. we determined the optimal value of boundary
parallel in regard to way length saving.
Combined navigation is possible to be applied only
provided that the orthodrome vertex is greater than the value of boundary
parallel (usually it is latitude 52 north or south) and that it is inside the
orthodrome, as well as provided that departure and arrival points latitudes are
less than the values of boundary parallel values.
The difference in distance in case of combined
navigation and orthodrome navigation is decreased with the increase of boundary
parallel value, i.e. with its approaching the orthodrome vertex. Although this
could be regarded as desirable from the point of view of way length and time
saving, from the point of view of safety of navigation it is highly undesirable
since it includes navigation in areas of great risk.
Dependence of the difference in the distances in case
of combined and orthodrome navigation
on value of boundary parallel was obtain by statistic analyses (24):
(25)
Where
r represents
dependence of the difference in case of combined navigation and orthodrome
navigation,
Bp
represents value of boundary parallel and
a, b, c, d,
e represent coefficients.
CONCLUSION
This paper deals with the practical problem of route
optimization in deep-sea navigation. Practically, it is impossible to navigate
strictly following the orthodrome and thus it is divided into a definite number
of waypoints between which it is navigated along the loxodrome. This paper
provides an answer to the questions what number of waypoints may be regarded
as optimal, what the geographical coordinates of these waypoints are and what
the loxodrome courses and loxodrome distances between the adjacent waypoints
are. The conclusion is that the saving expressed in percentage varies in
accordance with the position of endpoints.
Software has been designed to solve the problem of
defining elements needed for combined navigation with the additional
possibility of following the dependence of way length of the boundary parallel
value.
Calculated values of navigation elements represent
route optimization in deep-sea navigation in a limited, mathematical sense. Final
decision-making, i.e. practical route optimization, is left to the navigator.
Therefore, further research in this area should be focused on the development
of back-up systems to assist the navigator in practical seamanship.
LITERATURE
[1] Benkovic
F.,Piskovec M.,Lako Lj. i drugi, Terestrička i elektronska navigacija,
Hidrografski institut ratne mornarice, Split, 1986.
[2]
Cammarata S., Reti neuronali, Etaslibri, Milano, 1997.
[3] Gupta
U.G., Management Information System,
A Managerial Perspective, West Publishing Company, 1996.
[4] Ghezzi
C., Jazayeri M., Programming Language Concept, 3rd Ed., John
Wiley&Sons, 1997.
[5]
Holsapple C.W., Whinston A.B., Deccision Support Systems - A
Knowledge-Based Approach, West Publishing Company, 1996.
[6] Hiller
E. S., Introduction to Operations Research, 6th Ed.,
McGraw-Hill, 1996.
[7]
Jackson P., Introduction to Expert Systems,
Addison-Wesley, 1986.
[8] Klenak
S., Perovic M., Primjena informacionih sistema u pomorskom transportu, Tehnika
4, II Kongres o saobracaju, Beograd 1999. (257-262)
[9] Rich
E., Knight K., Artificial Intelligence, 2nd
Ed.,
McGraw-Hill, Milano, 1991.
[10]
Stankovic Lj., Uskokovic Z., MATLAB, Epsilon, Montex, Podgorica,
1991.
[11]
Sciuto D., Buonano G., Fornaciari W., Mari L., Introduzione ai sistemi
informatici, McGraw-Hill, Milano,
1997.
[12]
Saranovic S., Dinamicko programiranje u optimizaciji rute prekookeanskih brodova,
magistarski rad, Fakultet organizacionih nauka, Beograd 1979.
[13]
Teodorovic D., Transportne mreze, Univerzitet u Beogradu, 1987.
COPYRIGHT
2004 DIRECTIONS MAGAZINE