Optimization of the Number of Orthodrome Waypoints

Preface:

This paper provides an answer to the questions - what number of waypoints may be regarded as optimal, what the geographical coordinates of these waypoints are and what the loxodrome courses and loxodrome distances between the adjacent waypoints are.The conclusion is that the saving expressed in percentage varies in accordance with the position of endpoints.

The original contribution of this work is software, which has been designed to solve the problem of defining elements needed for combined navigation with the additional possibility of following the dependence of way length of the boundary parallel value.

Calculated values of navigation elements represent route optimization in deep-sea navigation in a limited, mathematical sense.Final decision-making, i.e.practical route optimization is left to the navigator.Therefore, further research in this area should be focused on the development of back-up systems to assist the navigator in practical seamanship.

With the development of knowledge, this task became more complex and the need for ship guidance arose, not just safe guidance but also the one to take a specific route in the least time possible.This led to the development of methods for position coordinates defining using objects at sea, on land, in space and celestial bodies.At the same time, sophisticated equipment was developed for establishing ship-to-ship and ship-to-shore communication, as well as the calculation techniques for the elements of sailing.

Thanks to systems of position fixing and communication, all the necessary elements for route optimisation are now available to a navigator.With the aid of computer programes, by entering departure and arrival position coordinates, assuming favourable hydro-meteorological conditions in the sailing area, the navigator can determine all the elements relevant to sailing.In case the departure and arrival positions are far apart, the navigator will choose great circle or orthodrome navigation, if they are close, he will choose rhumb line or loxodrome navigation, and if at higher latitudes, i.e.at areas possibly dangerous to navigation, he will choose combined navigation.

EDITOR'S NOTE: To view the entire body of this paper, please click HERE. To view the appendices of the paper, please download the .pdf file (756k) HERE. An abstract of the text appears below.

Abstract: This paper, in the original way, deals with the problem of orthodrome waypoints number optimization based upon minimization of saving in way length in case of strictly following orthodrome. In the cases of orthodrome intersection with Greenwich and Equator, the problem is solved in a way that orthodrome is divided into two segments, one between departure and intersection point, and another between intersection and arrival point.After that this two segments are optimized separately. Since by strictly following orthodrome some area dangerous to navigation could be reached, the problem of combined navigation is also solved by appropriate computer program in means of optimal boundary parallel value selection.

Key words: Routing, Optimization, Sailing, Orthodrome, Loxodrome, Waypoints

1.INTRODUCTION

In the early days of sailing, the main objective of a ship navigator used to be simply to take a ship from one point to another using as safe a route as possible.This used to be done on the grounds of personal experience and knowledge of the navigator himself, knowledge of land objects and celestial bodies, as well as the knowledge of periodically of hydrometeorological conditions.Multiple sailing following the same route and experience thus gained were the basis for safe ship guidance.

The paper presents the problem of route optimisation in practical navigation, by determining the optimal number of waypoints to which an orthodrome is divided and between which the loxodrome navigation is done.The optimal number of orthodrome waypoints depends upon geographical coordinates and the distance between the end points.

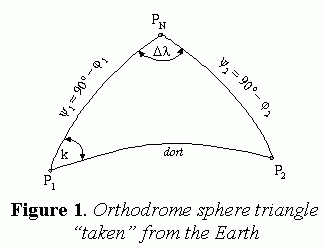
2.ORTHODROME AND LOXODROME

Sailing between two positions far apart in vast sea areas is possibly done in three ways: orthodrome, loxodrome and combined navigation.
The shortest route from departure position to arrival position is a shorter section of the great circle arc, i.e.orthodrome.Such navigation is difficult to achieve since the orthodrome cuts the meridians at different angles.It would require constant, precisely defined, change of course.

In the case ship course is constant, which is easily achievable in practice, the ship follows a curve asymptotically approaching the pole.Such a curve on the surface of the Earth is called a loxodrome.

In the case of combined navigation, a standard orthodrome is replaced by two-orthodrome tangent to the boundary parallel and one loxodrome between them.By applying the techniques of combined navigation, the areas of dangerous sailing, which could be reached by following strictly the orthodrome navigation, are avoided.
This paper deals with the practical problem of route optimization in deep-sea navigation.Practically, it is impossible to navigate strictly following the orthodrome and thus it is divided into a definite number of waypoints between which it is navigated along the loxodrome.